전도 방정식, Conduction equation을 기존의 x, y, z 공간 좌표계가 아닌 반지름 방향계, Radial system이나 원통 좌표계, Cylinderical coordinate에 적용하여 해당 시스템에서의 열전도와 열저항을 구할 수 있습니다.
반지름 방향계 열전도 방정식, Radial system heat conduction equation
앞선 포스트의 마지막 부분에서 언급한 원통 좌표계, 반지름 방향계에서의 열전도 방정식(Heat conduction equation)을 이용합니다.
열전도 방정식 경계조건, Heat Conduction Boundary Condition
열전도 방정식 경계조건, Heat Conduction Boundary Condition
미분방정식인 열전도 방정식을 풀이하기 위해서는 경계조건(Boudary condition)과 시작조건(Initial condition)이 필요합니다. 경계조건과 시작조건의 개수는 열전도 방정식의 차원(Dimension)에 따라 달라
in-foman.tistory.com
아래와 같은 반지름 방향계의 열전도 모델이 주어졌을 때 온도 분포를 구해보도록 하겠습니다.
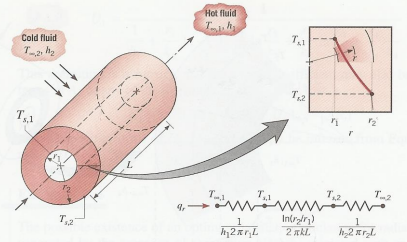
반지름 방향계의 열전도 방정식은 다음과 같습니다.
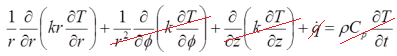
에너지 생성(heat generation)은 0이고 정상상태(Steady-state)이므로 우변의 Transient term도 0입니다. 우리가 관심 있는 좌표축은 r이므로 나머지 좌표축에 대해서도 0을 적용합니다.
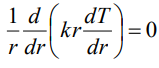
r에 대한 식만 남게됩니다. 이때, k가 상수라면 양변을 r에 대해 적분한 결과는 다음과 같이 얻을 수 있습니다.
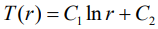
이 식을 풀기위해서는 2개의 경계조건(Boundary condition)이 필요합니다. 경계의 두 지점의 온도를 다음과 같이 정하겠습니다.
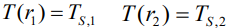
이 두 경계조건을 식에 대입하여 풀면 반지름 방향계의 온도 분포는 다음과 같이 나타낼 수 있습니다.
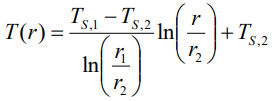
반지름 방향계 열저항, Radial system thermal resistance
열저항을 구하기 위해 원통의 면적을 구하면 원통의 면적은 원의 넓이에 높이를 곱하면 됩니다.
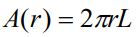
구한 면적을 다음 열전달률(Heat transfer rate)식에 대입합니다.
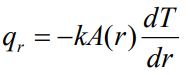
이때, dT/dr은 앞에서 구한 T(r)식을 r로 미분해보면 알 수 있습니다.
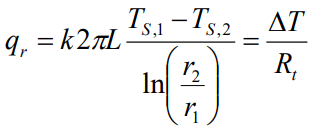
위 식을 열저항에 대해서 정리하면 원통 좌표계의 열저항은 다음과 같이 나타낼 수 있습니다.
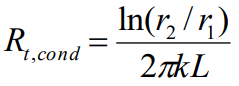
반지름 방향계 열전달계수, Radial system heat transfer coefficient
다음과 같은 반지름 방향계 열전달 예시가 있습니다.
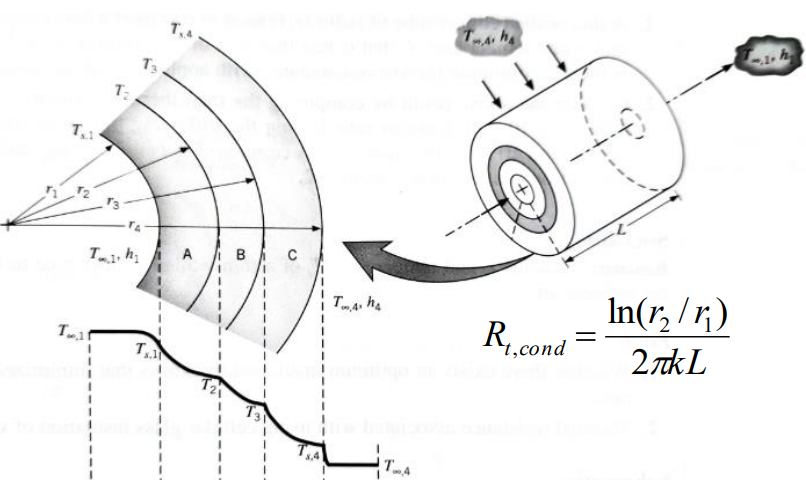
가장 안쪽과 바깥쪽의 빈공간과 표면 사이에는 대류(Convection)가 일어납니다. 따라서 아래의 대류의 열저항식을 사용하여 저항을 구할 수 있습니다. 전도, 대류, 복사의 열저항식은 앞선 포스트에서 다루었습니다.
평면벽 전도의 열저항, Thermal Resistance Of Conduction
전도의 열저항, Thermal Resistance Of Conduction
열저항이란, 영어로 Thermal Resistance라고 나타내며 열의 전달을 방해하는 값을 말합니다. 우리가 익히 알고있는 전기저항(Electrical resistance)과 같은 개념이라고 생각하면 쉽습니다. 왜나하면 열전
in-foman.tistory.com
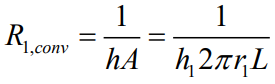
내부에서는 전도(Conduction)가 일어나므로 아래 전도의 열저항식을 이용합니다.

대류와 전도의 식에 각각의 반지름과 열전도도(Thermal conductivity)를 대입하면 됩니다.
직렬연결 형태로 구했으므로 모든 저항을 더해 전체의 저항을 구하면 열전달률(Thermal transfer rate)을 구할 수 있습니다.
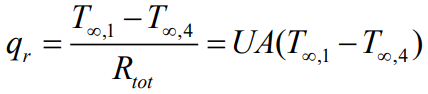
U는 전체의 열전달계수(Heat transfer coefficient)입니다.
'공대 공부 > 열역학, 열전달' 카테고리의 다른 글
| 단열재 임계 두께, Critical Insulation Thickness (0) | 2021.10.29 |
|---|---|
| 다공성 물질, Porous media (0) | 2021.10.28 |
| 열접촉저항, Thermal contact resistance (0) | 2021.10.26 |
| 열저항 직렬 병렬 복합벽, Thermal Resistance Parallel and Series (1) | 2021.10.25 |
| 평면벽 전도의 열저항, 대류, 복사 열저항 Thermal Resistance Of Conduction (0) | 2021.10.24 |

Comment