단층 신경망의 머신러닝과 다층 신경망의 딥러닝은 데이터를 학습함으로써 정답을 찾아가는 길, 즉 가중치를 찾아가는 알고리즘입니다. 단어 자체에 Learning(배우다)가 사용된 이유라고 할 수 있습니다.
처음 신경망에 대해서 설명드리면서 보여드렸던 그림을 다시 가져와봤습니다. 신경망은 결과값에서 오차를 찾아내어 학습 규칙에 따라 이를 다시 학습하여 정답을 찾아가는 것을 확인할 수 있습니다.
신경망은 뇌와 유사하게 정보를 데이터 사이의 가중치 ω로 저장한다고 말씀드렸습니다. 새로운 데이터를 학습해 나감에 따라서 가중치를 학습 규칙에 따라서, 체계적으로 바꾸어 나가게 됩니다.
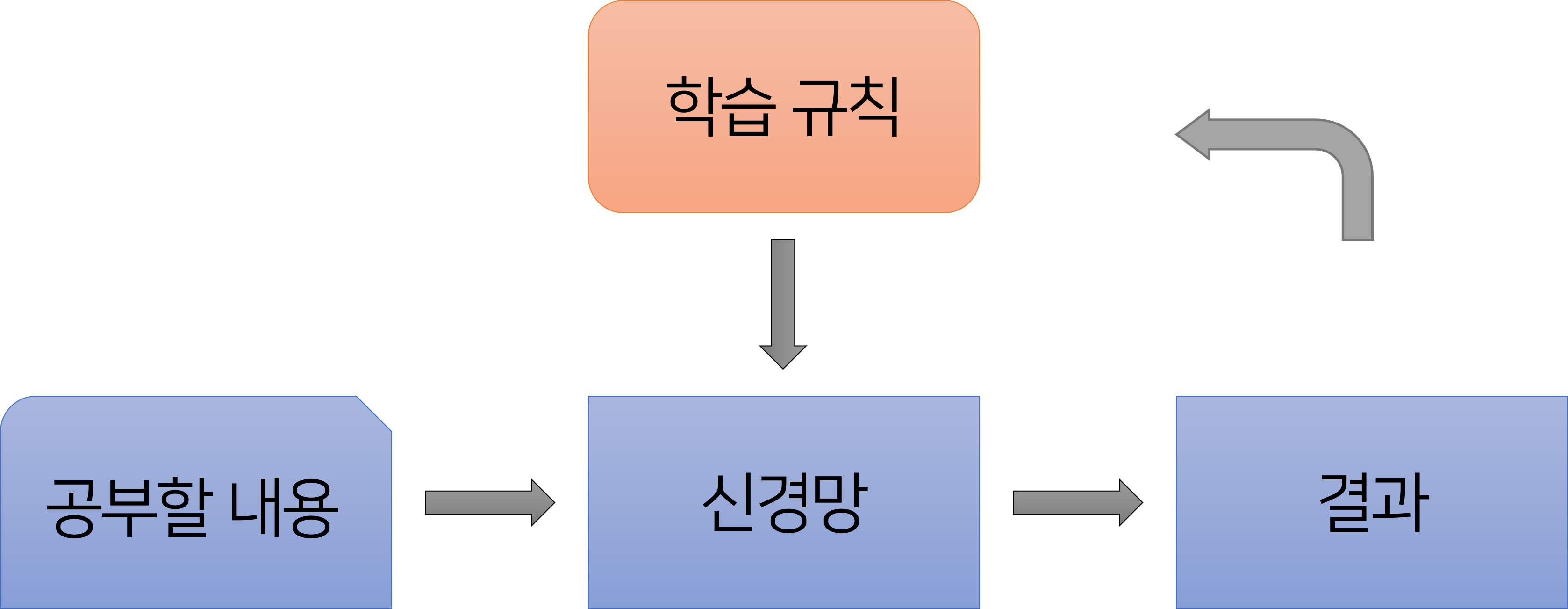
이 때, 신경망의 학습 규칙중에서 대표적이면서도 가장 기본적인 방법이 바로 델타 규칙입니다. 혹시 여기까지의 내용이 명확하게 와닿지 않는다면 이전 포스트를 참고하시기 바랍니다.
단층 신경망의 델타 규칙
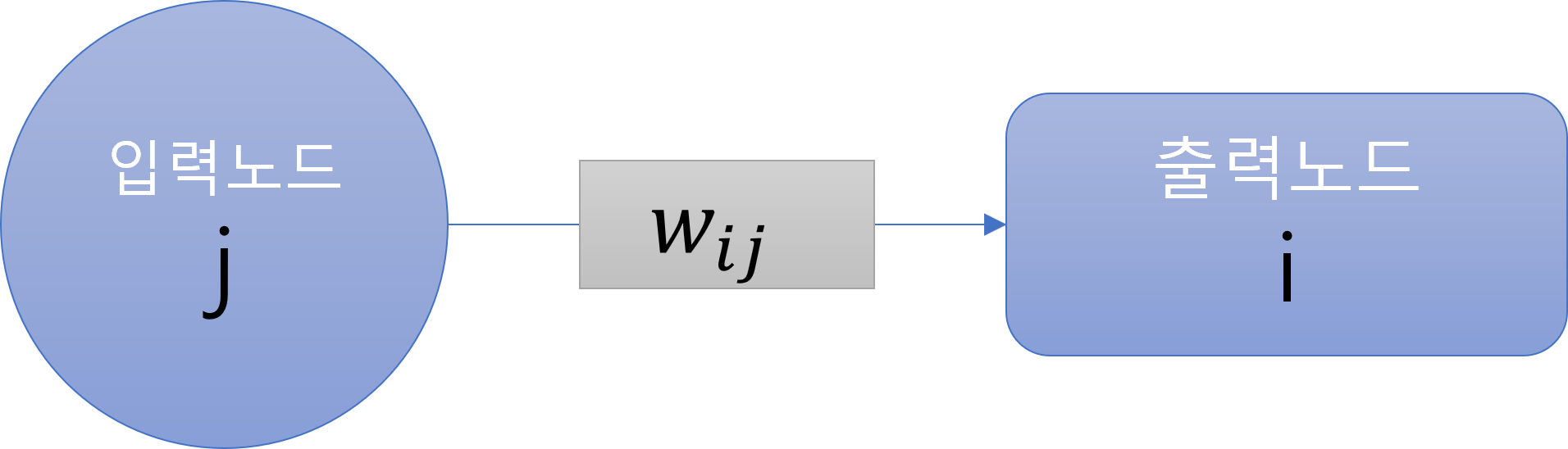
위 그림과 같은 단층 신경망을 생각해보겠습니다. 이 때, 입력노드 j가 출력하는 입력 값은 x_j 이고, 출력노드 i에서 출력하는 결과값을 y_i라고 하겠습니다.
그럼 단층 신경망의 델타 법칙은 다음 식으로 나타낼 수 있습니다.
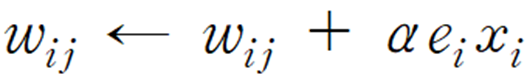
즉, "새로운 가중치 ω는 이전의 가중치 ω + αex 로 나타낼 수 있다."
새로운 가중치가 무엇일까요?
앞서 말씀드린대로 신경망은 데이터 사이를 연결하는 가중치 ω의 최적값을 찾아가는 과정이라고 말씀드렸습니다. 따라서, 그 신경망의 학습 규칙인 델타 규칙은 계속해서 새로운 ω값을 찾아갑니다.
그 때, 구하는 새로운 가중치 ω가 이전의 ω에 αex를 더한 값이라는 의미입니다.
이 때, 모르는 문자가 두 개 등장합니다. 바로 α와 e입니다.
α는 학습률을 뜻합니다. 0<α≤1 의 범위를 가지며 학습을 통해 변하는 ω값의 변화정도라고 생각하시면 됩니다. 학습률은 내가 임의로 설정해주는 값으로 학습률 α를 높게 설정하면 부정확하더라도 빠르게 정답을 향하고, 작게 설정하면 정확하지만 시간이 오래 걸릴 수 있습니다.
따라서, 우리는 학습률 α를 적절한 값을 설정하는 것이 중요한데, 정답이 존재하지 않고, 사례에 따라 그 값이 달라지기 때문에 직접 시행하면서 적합한 α값을 찾아가는 것이 중요합니다.
그리고 e는 오차로 e = 정답 - y 입니다. 즉, 실제 정답값과 현재 결과값의 차이를 말합니다.
이제 몰랐던 문자들에 대해서 알았으니 단층 신경망의 델타 법칙을 다시 정의할 수 있습니다.
"새로운 가중치 ω는 이전의 가중치를 오차 e에 비례하여 조절한다."
학습률 α와 입력값 x는 미리 설정해둔 값이기 때문에 위와 같이 말할 수 있는 것입니다.
이 델타 법칙을 단층 신경망이 학습 규칙으로 하였을 때, 학습 과정은 다음과 같습니다.
1. 초기 신경망의 가중치를 임의의 값으로 입력한다.
2. 해당 가중치를 이용하여 결과값을 도출한 후 정답과의 오차를 구한다.
3. 델타 규칙에 따라 새로운 가중치를 구해 다시 입력한다.
4. 충분히 만족스러운 결과값이 나올 떄 까지, 2번과 3번 과정을 반복한다.
다층 신경망의 델타 규칙
다층 신경망의 델타 규칙 식은 다음과 같습니다.
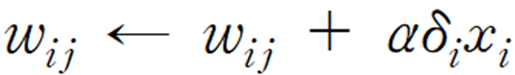
"새로운 가중치 ω는 이전의 가중치 ω + αδx 이다."
단층 신경망의 델타 규칙과 비교했을 때, 바뀐점은 e가 δ로 바뀌었다는 것입니다.
δ는 다음과 같이 정의합니다.
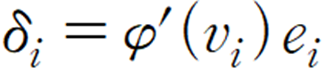
φ`는 활성화 함수의 도함수, υ는 가중합, e는 오차를 뜻합니다.
활성화 함수 φ는 신경망 모델에 따라서 다르게 설정되는 출력 값 변환 함수를 말합니다. 저의 경우에는 시그모이드 함수를 활성화 함수로 취하도록 하겠습니다.
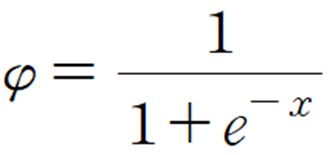
활성화 함수에 대해서는 이전 포스트에서 자세하게 다루었으니 참고하시기 바랍니다.
다층 신경망의 활성화 함수
다층 신경망은 은닉층, Hidden layer를 가지는 딥러닝 모델로 단층 신경망보다 정교하며 방대한 양의 데이터를 학습할 수 있다고 말씀드렸습니다. 하지만, 이전에 보았던 예시는 활성화 함수가 적
in-foman.tistory.com
시그모이드 함수의 특성상 도함수 φ`=φ(1-φ) 입니다.
그리고 가중합 υ는 각각의 데이터에 가중치를 곱한 후에 더한 합을 말합니다. 다시 말하자면, 활성화 함수를 적용하지 않은 원래의 결과 값입니다.
결과적으로 우리가 구하던 δ=φ(v)(1-φ(v))e 입니다.
혹시 헷갈리실까봐 적어두자면 φ는 함수이기 때문에 x값 대신, 가중합 υ를 대입한 것을 φ(v)로 나타낸 것입니다.
최종적으로 다층 신경망의 델타 규칙은 다음과 같이 유도됩니다.
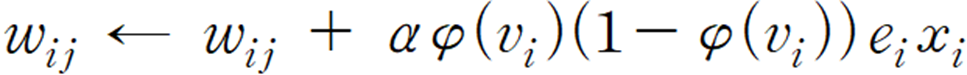
구하는 식이 복잡해보이지만, 사실 우리가 직접 계산할 일은 없기 때문에 단층 신경망이든 다층 신경망이든 델타법칙은 오차에 따라서 가중치를 조절한다는 점만 알고 계시면 되겠습니다.
쉽게 이해하는 단층 신경망
Neural Network, 신경망은 머신러닝의 모델 중 하나입니다. 4차 산업혁명 시대에 접어들어, 인공지능, 머신러닝, 딥러닝 등이 주목을 받으면서 중요해진 개념이 신경망입니다. 머신러닝의 수많은 모
in-foman.tistory.com
쉽게 이해하는 다층 신경망 딥러닝
앞에서 배운 머신러닝 단층 신경망은 사실 진정한 의미에서 신경망이라고 보기는 어렵습니다. 인간의 뇌와 같이 사고하고 정보를 저장한다기에는 연결관계가 너무나도 단촐했기 때문입니다.
in-foman.tistory.com
'공대 공부 > 딥러닝 신경망' 카테고리의 다른 글
| 다층 신경망의 활성화 함수 (0) | 2022.03.31 |
|---|---|
| 쉽게 이해하는 다층 신경망 딥러닝 (0) | 2022.03.31 |
| 쉽게 이해하는 단층 신경망 (0) | 2022.03.31 |

Comment